Большая часть деятельности менеджера-практика сосредоточена вокруг принятия решений. Более того, Г.Саймон и его школа [1] утверждают, что, принятие решений, и есть собственно, деятельность менеджера, а все остальные действия к ним прилагаются. Пусть данное мнение несколько утрировано, но оно реально отражает важность данного вопроса для менеджеров. Поэтому любое продвижение по пути создания исходных посылок для принятия решения будет облегчать деятельность практиков и создавать условия для более обоснованных действий.
Перед каждым менеджером практически ежедневно и ежечасно встают проблемы принятия решения. Мы не можем «отмотать ленту времени назад» и проверить, какое решение лучше, а какое - хуже. Приходится «писать с чистого листа». Поэтому, любой менеджер мечтает о некоем подспорье в этом вопросе.
Вариантов предложено достаточно много, начиная с «золотого правила коммерции», заключающемся в максимизации прибыли. В литературе описано несколько подходов к принятию решения. В частности, в качестве исходных предпосылок используют платежную матрицу, вероятностный анализ, исследование операций, финансовый контроль несколькими методами [2]. Кроме того, упоминают также спонтанный способ принятия решений, интуитивный метод, «золотое правило коммерции» (прибыль любой ценой), правило «плохой погоды» (ориентация на наихудший вариант условий реализации решения), формальную логику, процесс принятия бинарного решения, «дерево» решений, моделирование, прогнозирование с использованием различных подходов, теорию игр, теорию очередей, функционально-стоимостной анализ, экономические методы максимизации прибыли, расширения доли на рынке, экономии ресурсов, и метод оптимизации критериев [3].
В этом потоке предложений нетрудно и потеряться. Для того, чтобы этого не произошло, нужно следовать следующим правилам.
Выбрать цель изменений, которые станут следствием принятых решений. Даже «нулевой вариант», по которому ничего не происходит, тоже дает некоторые последствия. Такой целью может стать, и уже упоминавшаяся максимизация прибыли, и увеличение доли рынка, завоевание новых рынков, внутреннее развитие фирмы и т.д. В любом случае следует соизмерять поставленную цель с общественной пользой. Практика показывает, что фирмы, которые в своей миссии ориентируются только на «финансовое благополучие акционеров и сотрудников», долго не живут.
Часто используют такой прием, который заключается в составлении функции желательности Харрингтона [4]. Кроме того, используется также понятие целевой функции [5]. В этом же источнике представлены и другие методы принятия решений.
Метод оптимизации критериев заключается в том, что вначале моделируется искомый (желательный) результат, который раскладывается на отдельные составляющие (критерии). Далее на основании этих критериев моделируются процессы поблочно, с объединением блоков для достижения результатов.
Применение данного метода на практике встречает значительные трудности именно из-за необходимости разбиения принимаемого решения на блоки (нельзя обеспечить заведомо наилучшее или, хотя бы, приемлемое, разбиение на блоки) и сложности раздельного анализа критериев.
Исходя из этого, в рамках общей модели принятия решений по Г. Саймону, предлагается использовать нижеследующую процедуру.
Для этого в схеме Г. Саймона нужно разделить второй этап (выбор вариантов) на два подэтапа. Один из них будет собственно выбором вариантов между различными решениями, различающимися типологическими показателями. Второй должен представлять из себя, по существу, оптимизацию параметров выбранного варианта решения. Без второго этапа, в некоторых случаях, результат выбора по первому варианту может оказаться прямо противоположным тому, что от него ожидалось.
Первый этап обычно реализуется с помощью матрицы сравнения вариантов, причем она может простираться в своей сложности от самой простой, с «плюсами» и «минусами» в ячейках, до самой достоверной, с весовыми оценочными коэффициентами. Здесь также возможны различные варианты реализации, однако, с целью исключения методологических ошибок, в особенности, при принятии дорогостоящих и важных решений, лучше прибегать к следующей последовательности действий:
- составить перечень всех возможных параметров (характеристик и их числовых показателей) для оценки вариантов, включая неэкономические стимулы [6], с привлечением опыта организации, квалифицированных специалистов и литературных данных;
- выбрать критерии исключения параметров из списка;
- методом последовательного исключения параметров на основании принятых критериев удалить часть критериев и повторять последовательно эту процедуру до тех пор, пока оставшиеся параметры не будут хотя бы приблизительно равны с точки зрения требований критериев;
- составить матрицу сравнений;
- определить средние квадратичные отклонения для показателя в каждой ячейке;
- провести сравнение средних квадратичных отклонений по каждому столбцу с использованием критерия Кохрена [7] , представляющего из себя отношение среднего квадратичного отклонения изучаемого показателя к сумме всех средних квадратичных отклонений (в данном случае, к сумме по столбцу);
- исключить «выпадающие» по критерию Кохрена показатели, и нормировать (разделить) все показатели в каждом столбце таблицы на среднее значение каждого показателя по строке, а затем на сумму квадратов показателей, оставшихся в данном столбце после исключения «подозрительных» показателей;
- просуммировать показатели по каждому столбцу (варианту решения);
- произвести сравнение вариантов, выбирая вариант с наибольшим или наименьшим (в зависимости от заранее выбранного общего направления шкал показателей) значением суммы показателей по столбцу.
Представленная выше последовательность действий может показаться, на первый взгляд, «зубодробительной», но даже однократное ее практическое применение покажет, что это далеко не так и после первого опробования претворять в жизнь данную схему будет очень легко.
Чтобы облегчить восприятие предложенного алгоритма принятия решения, приведем пример его практической реализации.
Несколько лет назад крупная инвестиционная компания, рассмотрев итоги своей деятельности, приняла разумное и взвешенное решение об инвестировании части средств в научно-технические разработки. К рассмотрению были приняты четыре основных проекта, данные для которых сведены в матрицу сравнения, представленную в Табл.1.
| Варианты
Характеристики | Производство комбикормов | Получение топлива из неделовой древесины | Переработка отходов производства | Разработка и производство средств связи | Среднее по строке |
| Объем капвложений, усл. ед. | 22 | 35 | 41 | 64 | 40,5 |
| Срок реализации, мес. | 8 | 12 | 8 | 14 | 12 |
| Срок окупаемости, мес. | 8 | 12 | 9 | 12 | 10,25 |
| Доля рентабельности,1-Р, доли единиц | 0,8 | 0,5 | 0,6 | 0,1 | 0,5 |
| Престижность проекта (экспертные оценки), 1-П,баллов по 10-бальной шкале | 9 | 8 | 8 | 2 | 6.75 |
Примечания:
1. В Табл.1 представлены средние значения характеристик.
2. Различные значения показателей в Табл. 1 получены при использовании разных способов их определения. Например, объем капиталовложений определялся путем суммирования затрат разработчиками, путем проведения аналогии с подобными разработками, путем оценки допустимости расходов и путем экспертных оценок.
3. При использовании критерия Кохрена исключены из нормирования два значения - третье сверху в первом столбце и второе сверху в третьем столбце. (Для упрощения таблица исходных данных и полученных на их основании погрешностей не приводится. Данные из таблицы использованы для вычисления критерия Кохрена и анализа погрешностей на предмет их «выпадения» из общего строя).
После проведения расчетов с исключенными для нормирования показателями Табл.1 приобретает вид, представленный в Табл. 2. ( показатели, исключенные при нормировании, в ячейках Табл. 2 сохраняются, так как иначе результаты суммирования были бы несопоставимы).
Таблица 2. Модифицированные показатели проектов
| Варианты
Характеристики | Производство комбикормов | Получение топлива из неделовой древесины | Переработка отходов производства | Разработка и производство средств связи | Среднее по строке после уточнения |
| Объем капвложений | 0,57 | 0,91 | 1,07 | 1,46 | 38,5 |
| Срок реализации | 0,71 | 1,05 | 0,71 | 1,24 | 11,33 |
| Срок окупаемости | 0,97 | 1,45 | 1,09 | 1,45 | 8,25 |
| Доля рентабельности, | 1,60 | 1,00 | 1,00 | 0,40 | 0,50 |
| Престижность проекта | 1,33 | 1.19 | 1,20 | 0,30 | 7,5 |
| Сумма показателей | 5,18 | 5,60 | 5,07 | 4,85 |
|
Из Табл. 2 видно, что наилучшими показателями обладает проект в последнем столбце, который и был принят к реализации.
Второй подэтап, как говорилось выше, требует оценки величин характеристик, например, объема вложений или достигаемой рентабельности. Для определения конкретных показателей можно воспользоваться методом аппроксимирующих оценок. В рассмотренном примере таким конкретным показателем для инвестора являлся темп финансовых вложений, так как объем вложений был определен ранее путем сравнения вариантов в Табл. 2.
Здесь действуют две противоположно направленные тенденции. Инициаторы проекта, которым впоследствии придется отчитываться за вложенные средства, хотели бы получить их как можно раньше, чтобы застраховаться от всяких неприятных неожиданностей, как например, прекращения финансирования до окончания проекта. Инвесторы, наоборот, склонны «придерживать» средства, справедливо полагая, что их стоимость по мере перемещения по оси времени ближе к началу проекта возрастает. К тому же «быстрые» и объемные вложения, в некоторых случаях, могут приблизить к истощению основной источник финансирования самой инвестиционной компании, так как, чаще всего, поступления от него имеют равномерный характер.
Для простоты примем в качестве первой из гипотез для дальнейших рассуждений исходный помесячный темп вложений равным 1/12 полного объема ассигнований на программу (для целей статьи конкретные показатели не важны, поэтому все величины приводятся как условные, хотя, для определенности, можно отметить, что полный объем вложений составлял сотни млн. руб. в тогдашнем масштабе цен).
Равномерное помесячное вложение означает, что накопление вложенных средств идет по линейному закону:
Z=At+B (1)
где А и В – постоянные коэффициенты,
t – время с начала финансирования.
Здесь может рассматриваться несколько сценариев развития событий. Первый из них уже рассмотрен выше – это равномерное вложение средств с линейным нарастанием итога. Такой подход, как уже говорилось, вполне устраивает инвесторов, но может не устраивать инициаторов проекта. Если утрировать их притязания, то можно представить себе следующий «авантюристический» сценарий, достаточно часто, тем не менее, встречающийся в инвестиционной практике, особенно, в венчурной. В течение некоторого, пусть даже короткого промежутка времени, на начальном этапе, инициаторы проекта работают за счет собственных ресурсов, далее следуют значительные «вливания» средств от инвестора в течение довольно короткого промежутка времени, а затем темп инвестиционных вложений потихоньку сходят «на нет». Естественно, что такой подход (большие начальные вложения средств), пусть даже с начальным этапом реализации проекта без внешнего финансирования, не вполне может устроить инвесторов, его можно считать крайним проявлением возможных сценариев, далее которого инвесторы явно не пойдут и проект не будет реализован. Тогда функция, описывающая закономерность вложения средств инвестора в соответствии с данным сценарием, будет являться аппроксимирующей оценкой для данного проекта, ограничивающей максимальный темп вложений средств.
В качестве аппроксимирующей функции можно использовать довольно большое количество функций различных классов, но для простоты воспользуемся логарифмической зависимостью:
Z1=Clnt+D (2)
Если продифференцировать обе функции, то можно получить показатели удельного вложения средств помесячно. Для первого случая этот показатель равен А, для второго случая - 1/t.
Т.е. для последней функции вложения в начальный период достаточно велики, и постепенно спадают к концу инвестиционного периода. Каждый из проектов в рамках освоения комплекса продукции для полного удовлетворения запросов клиентов (в данном случае номенклатура изделий достигала 32 единиц) имеет определенную длительность (лаг) освоения. В соответствии с принятыми в инвестиционной и проектной практике правилами выбирают критический объект, от выполнения работ по которому будет зависеть и продажа остальных изделий, и для него определяют все показатели, включая погрешность аппроксимации. В данном случае таким объектом было коммутационное оборудование, а относительная погрешность аппроксимации была определена из условий практической реализации ( особенностей объекта) величиной не более 0,1 (здесь и далее, для удобства, все сравнения и оценки приводятся в относительных единицах).
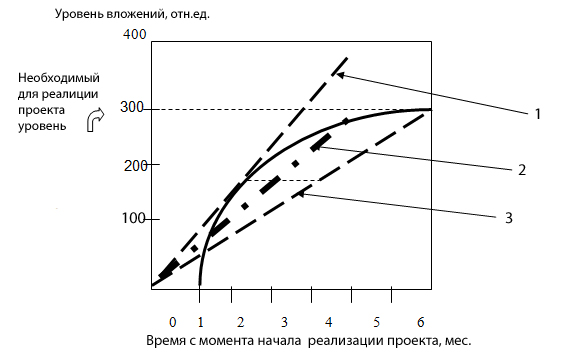
Результаты использования аппроксимирующей оценки представлены на Рис.1.
Здесь левая прямая 1 проведена по касательной к аппроксимирующей функции, и обозначает сценарий равномерных вложений, сам по себе приемлемый для инвесторов, но с неподходяще высоким, с их позиции, темпом вложений, правая прямая 3 представляет собой также сценарий равномерных вложений, но уже с темпом, не устраивающим инициаторов проекта, так как до искомого уровня вложений они «добираются» очень долго, хотя и одинаковое время с финансированием по «авантюристическому» сценарию (прямая 3 проведена через точку, в которой суммарные вложения по «авантюристическому» сценарию отличаются от необходимого уровня не более чем на величину заранее заданной погрешности). Занимающая серединное положение прямая 2 проведена через точку, представляющую среднее арифметическое соответствующих показателей по уровню вложений ( не по времени накопления вложений , так как это опасный путь, который может привести к срыву переговоров и прекращению работ по проекту). Среднее арифметическое как инструмент усреднения выбрано из условия равенства прав сторон на переговорах об инвестировании проекта.
При изменении коэффициентов С и D в формуле (2) расхождение между сценариями, а значит, и между прямыми 1 и 3, будет изменяться, в зависимости от кривизны аппроксимирующей функции, что делает ее удобным инструментом для аппроксимирующей оценки приемлемости каждого сценария.
В описанном выше случае переговоры привели к принятию предложенной модели выбора параметров решения, а использование выбранной аппроксимирующей оценки в сочетании с вариацией параметров аппроксимирующей функции позволило добиться расхождения между предложенными сторонами темпами инвестирования не более 10%.
Данный проект был реализован, но, по не зависящим от сторон причинам, инвестирование не было доведено до конца, и логического завершения проект не получил. Тем не менее, разработанные в его рамках изделия до сих пор успешно работают на сетях связи страны, и, по отзывам пользователей, заменять их на новые пока никто не собирается.
Использование предложенной последовательности действий, хотя и требует использования достаточно простого математического анализа, позволяет принимать обоснованные и взвешенные решения, вероятность достижения успешных последствий которых, как показывает опыт, достаточно велика.
Второй подэтап, как говорилось выше, требует оценки конкретных величин характеристик, например, объема вложений или достигаемой рентабельности. Для определения конкретных показателей можно воспользоваться методом двойных оценок. Сущность данного метода состоит в том, что участники переговоров или совещания, на котором необходимо принять решение, высказывают свои оценки для определяемой величины, задавая верхний и нижний предел, допустимый, по их мнению, для данного показателя проекта. При этом предполагается, что вероятность нахождения значения искомой величины в выбранных пределах подчиняется закону нормального распределения. Реально определить показатели распределения можно путем опросов членов каждой из делегаций на переговорах в качестве экспертов и вычисления соответствующих величин. Естественно, что оценки могут, и, зачастую, оказываются, полярными и, на первый взгляд, их свести нельзя. Далее участники совещания или переговоров высказывают и выслушивают различные соображения и сближают свои оценки до тех пор, пока области верхних и нижних оценок не пересекутся. При наступлении данного момента участники проекта останавливаются и оценивают вероятность того, что их оценки совпадают, используя известные формулы и таблицы для показателей нормального распределения. Если вероятность приемлемая (например, более 0,5 или 50%), то среднее верхних и нижних оценок для всех участников принимают в качестве конечной величины. Если стороны считают вероятность неприемлемо низкой, то процедура переговоров продолжается. Условно реализация такой схемы принятия решений по уровню величины рассматриваемой характеристики представлена на Рис.2.
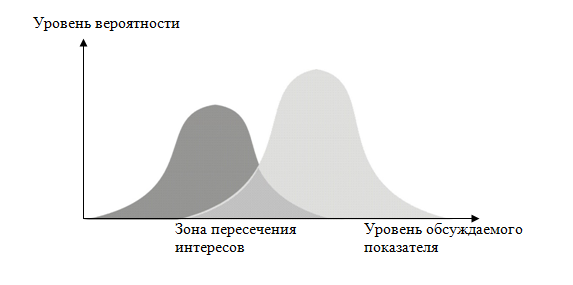
Процесс сближения вероятностных оценок представлен на Рис.3.
Рис.3.Пересечение вероятностных показателей для сторон в ходе принятия решения
Как показывает практика, такой метод принятия решения обеспечивает более быструю сходимость позиций сторон и более обоснованный выбор величины рассматриваемой характеристики, что весьма важно для дальнейшей деятельности организации.
Использование предложенной последовательности действий, хотя и требует использования некоторого, хотя и достаточно простого математического анализа, позволяет принимать обоснованные и взвешенные решения, вероятность достижения успешных последствий которых, как показывает опыт, достаточно велика.
Однако, если знания по ситуации повыше, то целесообразно поставить свою цель, то есть выгоду, какая бы она не была, и использовать платежную матрицу.
Список литературы
1. H.A. Simon. The New Science of Management Decision. N.Y., 1960. Цит. По кн. Д. Дункан «Основополагающие идеи в менеджменте».М.,1996.
2. Олдкорн Р. Основы менеджмента. М., «Финпресс», 1999, с. 299-301.
3. Бусыгин А.В. Эффективный менеджмент. М., «Финпресс», 2000, с.454-586.
4. Петров П.А. Формирование единой методологии контроллинга стратегического потенциала промышленного предприятия. Вопросы управления, №3(16), 2011, с.128-137.
5. Тополя И. В. Экономическая теория и модели целевой функции фирмы. Проблемы управления. №1, 2004, с.54-59.
6. Иноземцев В.Л. Современное постиндустриальное общество: природа, противоречия, перспективы. М., «Логос», 2000.
7. Дубров А.М. и др. Математическая статистика (для бизнесменов и менеджеров). М., МЭСИ, 1995.






 Скопировать ссылку
Скопировать ссылку